点乘
设两组向量
$latex a = (a_{1}, a_{2}, … a_{n}) $
$latex b = (b_{1}, b_{2}, … b_{n}) $
a和b的点乘公式为
$latex a\cdot b = a_{1}b_{1} + a_{2}b_{2} + … + a_{n}b_{n} $
点乘几何意义 - 1. 点乘的几何意义可以用来表征或计算两个向量之间的家教,如果a和b为单位向量,那点乘的结果就是两个向量夹角的正弦值
$latex a\cdot b = \left | a \right | \left | b \right | cos \theta $
2. 点乘的结果还可以看做是 第一个向量投影到第二个向量上(这里,向量的顺序是不重要的,点积运算是可交换的)
叉乘
设两组向量
$latex a = (x_{1}, y_{1}, z_{1}) $
$latex b = (x_{2}, y_{2}, z_{2}) $
a和b的叉乘公式为
$latex a \times b = \begin{bmatrix}
x_{1}\\
y_{1}\\
z_{1}
\end{bmatrix}\times \begin{bmatrix}
x_{1}\\
y_{1}\\
z_{1}
\end{bmatrix} = \begin{bmatrix}
y_{1}z_{2} - z_{1}y_{2} \\
z_{1}x_{2} - x_{1}z_{2} \\
x_{1}y_{2} - y_{1}x_{2}
\end{bmatrix} $
叉乘几何意义 - 叉乘得到的向量垂直于原来的两个向量。
$latex \left | a \times b \right | = \left | a \right | \left | b \right | sin\theta $
既然得到的是垂直两个向量的向量,那方向怎么算呢?
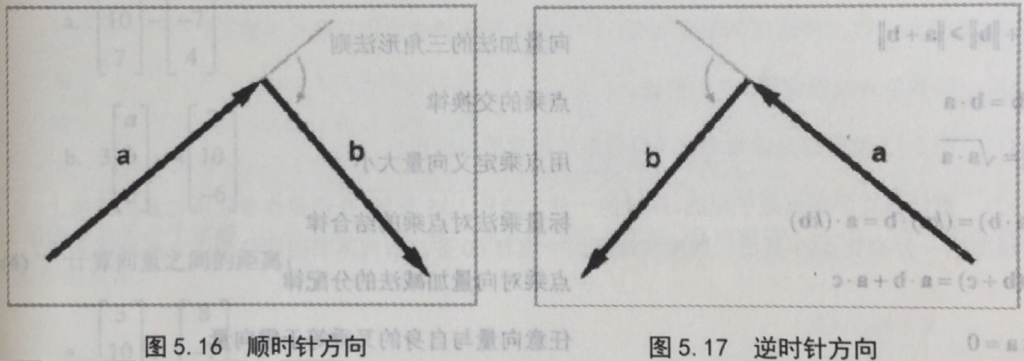
通过将a的头与b的尾相接,并检查从a到b是顺时针还是逆时针,能确定$latex a \times b $ 的方向。
在左手坐标系中,如果a和b呈顺时针,那么$latex a \times b $ 指向您,如果a和b呈逆时针, $latex a \times b $ 远离您。在右手坐标系中,恰好相反,如果a和b呈顺时针, $latex a \times b $ 远离您,如果a和b呈逆时针, $latex a \times b $ 指向您